最終更新: 2024/02/292024/02/29 追記 こちらの記事の内容について、2023.3以降の内容を反映し、また日本地図などの距離が近い場合についての方法について、以下の記事にまとめました。
よろしければ、こちらも参照ください。 距離が近い地図上の２点に曲線を描く
今回のテーマはCurved Line Mapです。要は地図に曲線を引きます。下記のViz作成を通して解説します。
以下の記事を参考にしました。
今回の記事に使用したワークブックは以下からダウンロードできます。
今回の記事に使用したデータセットは以下から入手できます。（昔のViz for Social Goodに使われたデータの様子？）
２．countries_codes_and_coordinates.csv （上記データに緯度、経度をJOINでくっつける用データ）
【必要なデータの形】
直線でも曲線でも、TableauでMap上に線を引くには、最低限「起点が何か」「終点が何か」「起点の緯度経度」「終点の緯度経度」の情報が必要です。
今回のデータセットから最低限欲しいのは以下の青帯のカラムです。
（起点と終点はISOコードか国名どちらかでいいです。）
また、ある起点と終点を結ぶ線を引くためには、ある経路に対して２つのレコードが必要になります。
したがって上記のようなテーブルをSelf-UNIONします。
緯度経度のJOINとSelf-UNIONをTableau上で行うと、下記のような構成になります。
結合条件はそれぞれdest.isocode = Alpha-3 code、orig.isocode = Alpha-3 codeです。
JOINの結果、起点と終点の緯度経度が得られるので、それぞれorig.lat, orig.lon, dest.lat, dest.lonとリネームします。
以上でTableauに読み込むためのデータ準備は完了です。
【Data Paddingについて】
今回に限らず、曲線をテーマにしたものでは「Data Padding」という概念がよく出てきます。
詳細は各自お調べしていただくとして、概要だけ説明します。
例として、以下の２値（１か１００）をとる計算式を用意します。ここでTable NameはSelf-UNIONの結果作られるカラムです。
1 or 100
IIF([Table Name] = "Destination_Origin",1,100)
この計算式からビンを作成します。
これを用いて、以下を作成してみます。
元の「1 or 100」が２値しかとっていないので、ビンを作成しても出てくるのはこの２つのビンだけです。
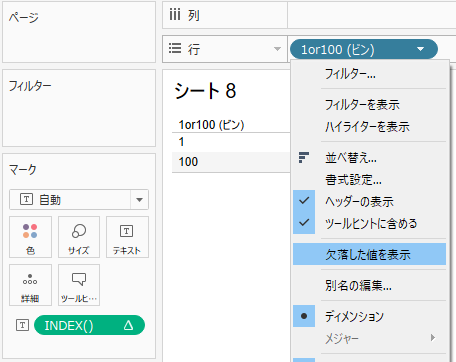
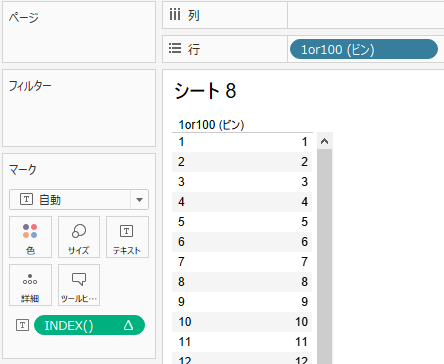
しかし「欠落した値を表示」すると、以下のように１から１００まで全てのビンが出てきます。
この「１から１００までの間を埋める（Padding）」ことを「Data Padding」と呼びます。
この結果何がうれしいかと言うと、本来存在しなかったデータとデータの間にも表計算が適用され、表計算の値が得られることです。
【計算フィールドの作成】
Data Paddingを念頭におきつつ、まずは必要な計算式をつらつら作成しておきます。
先にお断りをしておきますが、幾何学に詳しくないので、いくつかの計算式の導出は省略します。
Brezier Value (この後ビンサイズ１でビンを作成。[# of bins]は整数型パラメータ(100で設定)。)
IIF([Table Name] = "Destination_Origin",1,[# of bins])
INDEX
INDEX()
t
([INDEX]-1) / [# of bins]
Newlat1 Radians
RADIANS(WINDOW_MIN(MIN([orig.lat]),FIRST(),FIRST()))
Newlat2 Radians
RADIANS(WINDOW_MIN(MIN([dest.lat]),LAST(),LAST()))
Newlon1 Radians
RADIANS(WINDOW_MIN(MIN([orig.lon]),FIRST(),FIRST()))
Newlon2 Radians
RADIANS(WINDOW_MIN(MIN([dest.lon]),LAST(),LAST()))
ここで注釈を入れます。
・上記の表計算はすべてBreizier Value (bin)に沿って計算。
・Newlat、Newlonは単に起点と終点の緯度経度を、表計算形式で参照しているだけです。仰々しいですが大したことはしていません。
続いて上記から、起点と終点の「球表面に沿った2点間の距離」を計算します。
詳しくは下記Wikipediaを参照してください。
Distance
2*ASIN( SQRT( POWER((SIN(([Newlat1 Radians]-[Newlat2 Radians])/2)),2) + COS([Newlat1 Radians])
* COS([Newlat2 Radians])
* POWER((SIN(([Newlon1 Radians]-[Newlon2 Radians])/2)),2) ) )
このあたりから正直さっぱりなんですが、以下の式が必要なようです。
大学時代を思い出す、幾何学と線形代数ゴリゴリ感がしますね。
A
SIN((1-[t])*[Distance]) / SIN([Distance])
B
SIN([t]*[Distance])/SIN([Distance])
x
[A]*COS([Newlat1 Radians])*COS([Newlon1 Radians]) + [B]*COS([Newlat2 Radians])*COS([Newlon2 Radians])
y
[A]*COS([Newlat1 Radians])*SIN([Newlon1 Radians]) + [B]*COS([Newlat2 Radians])*SIN([Newlon2 Radians])
z
[A]*SIN([Newlat1 Radians]) + [B]*SIN([Newlat2 Radians])
最後に、これら計算フィールドを使用して、「2点間を結ぶ球面上の線の緯度経度」を度数法（Degree [°]）で記述します。
Newlat
DEGREES(ATAN2([z],SQRT(POWER([x],2)+POWER([y],2))))
Newlon
DEGREES(ATAN2([y],[x]))
これで計算式は準備完了です。
【Curved Line Mapを作る】
やっと本題です。以下のように配置すれば、基本のCurved Line Mapが作成されます。
このとき、Brezier Value (Bin)に欠損値を表示させることを忘れないようにしてください。
ここで、PATHはそれぞれの曲線を一意に定義するための計算フィールドです。今回の場合は以下のように作成しました。
PATH
[orig.name] +"-"+ [dest.name]
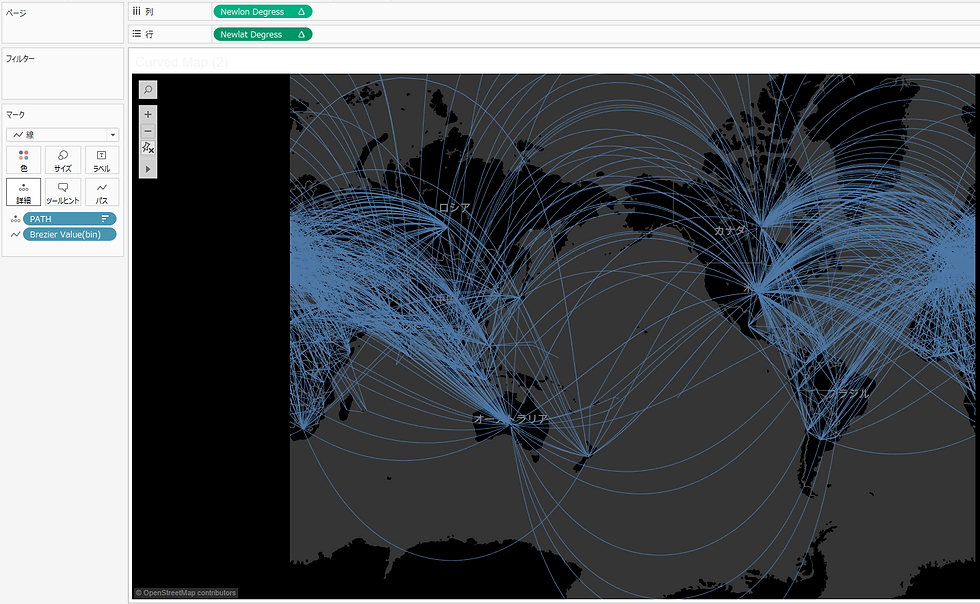
あとは良い感じに曲線のサイズ、色を決めてあげれば、下記のようなVizが作成できます。
比較のために直線バージョンの画像も載せます。曲線の方が今回のデータの場合は見やすいですね。
【おまけ１】
Data Paddingはちょっとイメージがつきにくいかもしれないので、下記のVizをワークブックにご用意しました。
・# of binsの大きさによって曲線がどのくらい粗くなるか
・Data Paddingと表計算によって、どのように曲線が作られているか
を触りながら確認するためのVizです。どうぞ遊んでみてください。
【おまけ２】
必ずしも直線が悪いということもないです。下記のVizは直線でも素敵ですよね。使い分けが大事かなと思います。
Reference: https://www.youtube.com/watch?v=ckQNNhCfUW4
Curved Line Mapいかがでしたか。
ご質問等はTwitter、Linkedinへよろしくお願いします。ただし幾何学の質問はだめです。