この記事は以下のSankey Diagram作成ガイドの続編であり、以下の記事を前提としています。
表題の通り、今回はSankey Diagramのアイテム間に余白を作る方法について解説します。
今回の記事に使用したWorkbookは以下からダウンロードできます。
基本方針
やり方は色々あると思いますが、今回は「ある大きさの余白を、各アイテムに分配し、Sankeyの両側で高さが変わらないように設計」します。
要は余白を用意して、右側or左側の(ディメンション内の個数-1)で等分して、差し込むイメージです。
ということで、余白のサイズはパラメータで用意するわけですが、この余白分だけSankeyに使用した様々な表計算、具体的にはMax/Min Positionあたりを修正しなければなりません。
この修正が若干厄介です。
例えば左側のオレンジの3本に注目します。
余白無しバージョンに比べ、各帯の位置が(2/3)余白だけ上にズレています。
更に具体的に言うと、各帯の下端と上端に、Sankeyの計算式の結果＋(2/3)余白が足されています。
逆に言えば、チャレンジはそこだけです。
分かってしまえば難しくはないはずです。きっと。
計算式を見る
ということで、最初に修正版の計算式を一通りお見せします。
Dimension 1についての式のみを挙げていますが、Dimension 2についても基本は同じです。Dimension 1と2を入れ替えてあげればいいだけです。
ここで[Margin]は数値型のパラメータです。
先に概要だけ説明すると
Wrapの式でRUNNING_SUMを取っているので、Dimension 1のアイテムで区別されたPolygonについて、各Dimension 1について1点だけMarginを与えるように設計しなければならない。これをLAST()を用いて制御（Margin 1の式のIIF()部分を参照）。
余白をDimension内のアイテム個数で等分（Margin 1の式の分母を参照）。
余白をMin/Max Positionに追加
RUNNING_SUMにより、余白が割り当てられている点は余白が2回アサインされてしまう。なのでWINDOW_MAX([Margin 1])で修正。
という流れになります。
正直なんのこっちゃという感じなので、一つ一つ見ていきましょう。
（ちなみに、今回はワークブックと記事を見ながら、手を動かしてみることを強くオススメします。表計算は眺めるよりも作ってみる方が早いです。）
LAST 1とMargin 1について
LAST 1はシンプルにLAST()です。
LAST 1
LAST()
表計算を上記の表のように設定すると、下図のようにLAST 1はアサインされます（テキストラベル参照）。
このLAST 1を使ってMargin 1を計算します。
Margin 1
IIF([LAST 1] = 0,[Margin],0)
/MIN({COUNTD([Dimension 1])-1})
この計算フィールドの意味するところは「LAST 1が0であればMarginを等分した数値を割り当てる」です。
つまり、各色のPolygonについて、最上段Polygonの上端だけに余白が割り当てられます。
MIN/MAX POSITIONについて
続いてMin Positionについて見てみます。
Min Position 1 (margin)
RUNNING_SUM([Max for Min Position 1] + [Margin 1]) - [Sankey Arm Size]
ちなみにMax for Min Position 1は以下です。余白無しSankeyと同じです。
Max for Min Position 1
RUNNING_SUM([Sankey Arm Size])
上記については、単にMin Positionの中にMargin 1を追加し、合わせてRUNNING_SUMをとっているのみです。
ところで、実はこの式をそのままWrapに投げてしまうと、各Polygonの位置がおかしくなります（下図参照）。
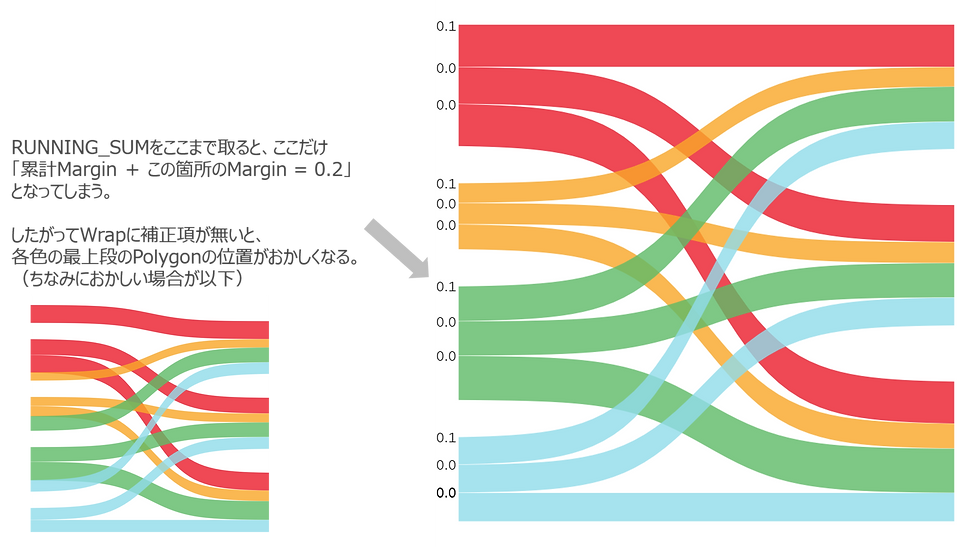
ということで、LAST 1 ＝ 0でMarginが重複している箇所について補正します。
Min Position 1 Wrap (margin)
WINDOW_SUM([Min Position 1 (margin)]) - WINDOW_MAX([Margin 1])
WINDOW_SUMで最終的に[Margin 1]が2回カウントされる形になるので、それぞれに割り当てられているMargin 1を、各Polygonの各点から引きます。
これを許しているのがPath Frameに沿ったWINDOW_MAX([Margin 1]) の補正項です。
（Path Frameに沿った計算であることが重要）
Max Positionについても同様の議論がされますので、計算式の紹介に留めます。
Max Position 1 (margin)
RUNNING_SUM([Sankey Arm Size] + [Margin 1])
Max Position 1 Wrap (margin)
WINDOW_SUM([Max Position 1 (margin)]) - WINDOW_MAX([Margin 1])
Sankey Polygonをつくる
Margin使用した上記の計算フィールドを、Sankey Polygonの式にそのまま使用します。
Sankey Polygons (margin)
IF [Path Index] > 49 // ポリゴンの上半分を描画
THEN [Max Position 1 Wrap (margin)]
+ ([Max Position 2 Wrap (margin)] - [Max Position 1 Wrap (margin)])
* [Sigmoid]
ELSE [Min Position 1 Wrap (margin)]
+ ([Min Position 2 Wrap (margin)] - [Min Position 1 Wrap (margin)])
* [Sigmoid]
END
このあとのVizの作り方は、前回の記事と全く同じなので割愛します。
ここまでで余白つきSankey Diagramは完成です。
SANKEY DIAGRAM両端のラベルを作る
最後の仕上げです。Sankey両端、Dimension 1とDimension 2を作成するラベルを作成します。
先に概観だけお見せすると、Gantt Cahrtで作ります。
Bar Size
-[Chosen Measure]/TOTAL([Chosen Measure])
Bar 1
RUNNING_SUM([Chosen Measure]/TOTAL([Chosen Measure]))
+[Margin] / MIN({COUNTD([Dimension 1])-1}) * (INDEX()-1)
Bar Sizeは、Dimension 1の各アイテムの、全体における割合を示しています。
Bar 1は「全体における割合」の累計（RUNNING_SUM）を出した後に「等分された余白×Dimension 1の累計アイテム数」を足しています。
累計はINDEXで行いましたが、このあたりの実装はもう少し分かりやすくできそうですね。
Gantt Chartにラベルを付けてもいいのですが、あえて別ワークシートを作成し、ラベルを工夫してみます。こういう実装もできますよね、ということで。
透明なGantt Chartを用意します。
ここでLabel用に位置を調整した計算フィールドを用意します。
Bar 1 (Label)
[Bar 1] - [Chosen Measure]/TOTAL([Chosen Measure])/2
要は「Bar 1から割合の半分を引く→Ganttの位置が、Bar 1に比べて半分になる」というだけです。
Bar 1とBar 1 (Label)を並べた結果がこちらです。
同様のものをDimension 2にも作ってあげれば、以下のようにSankey Diagramが作成できます。
最後に
念願の「前処理不要のSankey Diagramに余白を付ける」ことに成功しました。
余白のパワーは偉大で、やっぱり見やすくなるんですよね。
計算フィールドも余白無し版に比べて大きな修正はないので、今後はこちらをスタンダードにしていこうと思います。
ご質問等はTwitterまたはLinkedinまでよろしくお願いします。 それでは。