今回のテーマはDendrogramです。要は樹形図です。
異なるディメンション間の関係性を見る際に便利な可視化手法です。
Dendrogram記事は3部作構成にしようと思います。
基本編:とりあえず線を引いてDendrogramを描く
応用編1:項目選択時に、その項目と関連項目をハイライトする
応用編2:線に数値情報を与え、かつ選択項目でハイライトする
今回は基本編として、まずはDendrogramの形を作るところから始めます。
今回の記事に使用したWorkbookは以下からダウンロードできます。
データはTableau Desktop2019.3版のSample Super Storeです。
Dendrogramのモチベーション
3つの側面があるかなと思います。
(Sankey Diagramと見た目、計算式が似るため比較します)
ディメンション間の関連性が見やすい
Sankey Diagramと異なり縦方向の項目間隔を一定にできるので、項目が多い場合にSankey Diagramより項目が見やすい
Polygonではなく線で表現するので、Server上での描画パフォーマンスがSankeyより優れる可能性がある(参考WhitePaper)
実際にやってみた例が以下です。
Tableau Serverの勉強として、License × Site Role × Permissionの関係性をまとめてみました。
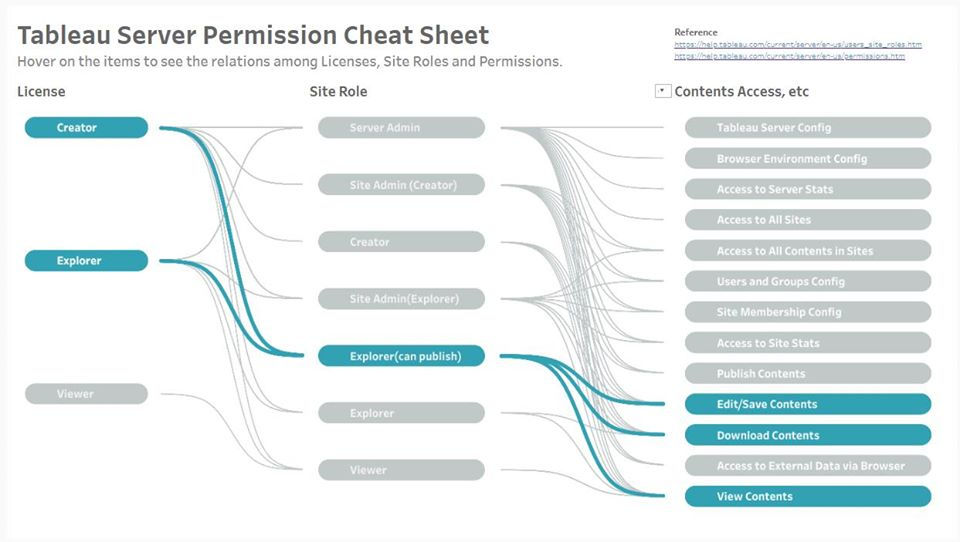
Tableau Public: https://tabsoft.co/2NPonQz
この可視化は「どのLicenseとSite Roleで、潜在的にどのPermissionが持てるか」のみに焦点を置いており、何かの項目を選択した際にハイライトで関連性を見やすくしています。
上記の例では関連性のみが焦点ですが、色や太さに数値情報を与えることにより簡易的なSankey Diagramのようにも機能します。
このような用途にDendrogramはとてもマッチします。
DENDROGRAMをつくる
早速作っていきましょう。第一歩はSelf-UNIONです。

次に以下の計算フィールド(ディメンション)を作成します。
(以降の計算式を一般化するためのものです)
Dimension 1
[Segment]
Dimension 2
[Region]
Dimension 3
[State]
PATH
IIF([Table Name]={MIN([Table Name])},0,97)
PATH(bin)
PATHを基にBinを作成(Bin Size = 1)
基本的な流れはSelf-UNION Sankey Diagram作成記事と同じです。
次に以下の計算フィールド(メジャー)を作成します。
INDEX 1
INDEX()
INDEX 2
INDEX()
INDEX 3
INDEX()
Divider 1
WINDOW_MAX([INDEX 1])
Divider 2
WINDOW_MAX([INDEX 2])
Divider 3
WINDOW_MAX([INDEX 3])
Path Index
INDEX() //Bin → 数値への変換
ここでINDEX1~3について、これらがDendrogramの各項目の位置に使用されます。
並べてみると以下のようになります。

今回Dimension 3の項目数が多いので、ちょっとスケールが合わせにくいですね。
したがって0~1の範囲に落とし込みます。そのために各Denominator 1~3を使います。

Denominator 1~3は各INDEX 1~3それぞれの最大値(WINDOW_MAX)を返すので、必ず0~1の範囲に収まります。これで各Dimensionの位置スケールが揃いました。
次に曲線を描くための計算フィールドを用意します。
T
IF [PATH Index] <= 49
THEN (([PATH Index] - 1) % 49) / [Param Divider] - 6 // -6 to 6
ELSE - (([PATH Index] - 1) % 49) / [Param Divider] + 6 // 6 to -6
END
Sigmoid
1 / (1+EXP(1)^-[T])
Curve 1-2
[INDEX 1]/[Denominator 1] //起点
+ ([INDEX 2]/[Denominator 2] - [INDEX 1]/[Denominator 1]) //終点
* [Sigmoid]
Curve 2-3
[INDEX 2]/[Denominator 2] //起点
+ ([INDEX 3]/[Denominator 3] - [INDEX 2]/[Denominator 2]) //終点
* [Sigmoid]
TとSigmoid関数については、こちらの記事中に詳しく解説してありますので、そちらをご参照ください。
Curveの式については、基本的にはSigmoid関数の基本性質のため割愛します。
要は起点から線を引き、終点をどの位置にするかという話です。
計算フィールドが揃いましたので、以下のようにそれぞれ配置します。
ここでPATH(bin)の欠損値表示オプションをオンにし、Data Densificationすることを忘れないようにしてください。

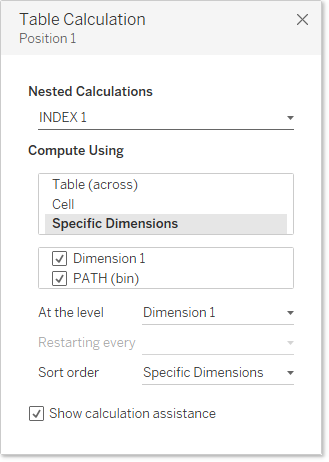
それぞれの表計算設定は以下の通りです。
Dimension 2-3間のCurveについても同様に配置します。

それぞれの表計算設定は以下の通りです。
ここで見た目の都合、Dimension 3 (State)に対して、Dimension 2 (Region)でソートをかけます。

それぞれの軸範囲を適当に揃えた後に、いったんダッシュボード上に配置してみます。

綺麗なDendrogramが描けました。
各Dimensionのラベルが欲しいので、それ用のSheetを作成します。
(難しい作りではないので、円マーク等で適宜お好みのラベルを作って下さい)
線マークで作成します。

表計算の設定は以下です。
Dimension 2, Dimension 3についても同様です。
各Dimensionにラベル用Sheetを作成し、配置すると以下のようなDendrogramが作成できます。

さて、Dendrogramの作り方は分かりました。
一方でこの図だけでは特に有用なインサイトは得られないため、実用的にするためにはもう少々工夫と計算が必要です。
その内容は次回以降で触れていきます。
ちなみに:計算を軽くするため直線で描く
ところでData Densificationを使用するたびに思うのですが、この手法はTableau上での(厳密にはSheet上の)マーク数を増やすので、基本的に描画パフォーマンスは落ちます。
そのため極力マーク数を増やさないために、直線で同じようなことをするという次善策も考えた方が良いかなと最近思ってきました。
今回の場合、以下のようになります(具体的な計算式はWorkbookを見て下さい)。

まあ悪くはないかな、という感じです。
Sankey Diagramも同様に四角形ポリゴンで描けるはずなので、パフォーマンス重視の計算方法もまとめた方が良いかもですね。近々やってみます。
(さらに言えば、Self-UNIONを使わずデータ量を増やさないという形でも改善できます。こちらの記事序盤の「Path Frame」の計算式をご参照ください)
最後に
Dendrogram基本編、いかがでしたか。
基本編と言いつつすでに難易度がやや高めですが、関係性を可視化する際に効果的な手法なので、ぜひチャレンジしてみてください。
次回から今回作成したDendrogramに実用性を与えていきます。