距離が近い地図上の2点に曲線を描く
- Yoshitaka Arakawa
- 2024年3月3日
- 読了時間: 8分
最終更新: 2024/03/03
参考資料
https://ja.wikipedia.org/wiki/%E3%83%99%E3%82%B8%E3%82%A7%E6%9B%B2%E7%B7%9A
https://www.f.waseda.jp/moriya/PUBLIC_HTML/education/classes/infomath6/applet/fractal/spline/
https://domoorewithdata.com/2022/11/01/fun-with-curves-in-tableau-part-2-controlling-bezier-curves/Tableau 2019.2にて地図上の2点をつなぐ線を描く、MAKELINE関数が実装されました。
この関数により地図を使った可視化の幅が広がりましたが、緯度経度が近い2点を結ぶ場合、ほぼ直線となります。
特に日本地図を用いた場合、ヘルプページ上の図にあるような曲線ではなく、ほぼ直線のみ描かれます。
この記事では近い2点を結んだ場合でも曲線を描く方法について記載します。
また曲線の長さをメジャーに合わせて変更する方法についても記載します。
今回使用したWorkbookは以下からダウンロードできます。
https://tabsoft.co/42SplRq サムネイルに使用したWorkbookは以下からダウンロードできます。
本記事の内容の応用として用意しました。
使用したデータは以下からダウンロードできます。
(転入者数の出典: 東京都住民基本台帳人口移動報告 令和4年 第5表)
MAKELINE関数の問題
冒頭で述べたように、このMAKELINE関数で描かれる線は、結ぶ2地点が近い場合は、ほぼ直線となります。
(MAKELINE関数の詳細については、こちらのがねこさん(@ritz_Tableau)の解説記事を参照ください)
例えば、以下は東京都と関東地方~東北地方までの都道府県を、MAKELINE関数を使用して線を描いた場合です。 (地点には都道府県庁所在地の緯度経度を使用しています)

少し文脈を加えるために、2022年1月の、東京都への転入者数を色に加えてみます。ここでは具体的な数値は上げませんが、色が濃いほど転入者数が多いことを示しています。

転入者数は神奈川県、埼玉県、千葉県が特に多かったのですが、その3県は東京都に近いため線が短く、この地図上では目立ちにくくなっています。
またそれぞれの直線が近い場合や重なった場合の可読性や、特定の線をクリック等で選択することも難しくなっています。
以下では、関東~九州地方でフィルタした場合で例示しています。
この問題を解決するために、この記事では以下を達成することで、東京都への転入者数が多い都道府県を視覚的に分かりやすくすることをゴールとします。
直線ではなく曲線で描画する
また曲線の長さ(より具体的に言えば、直線距離と曲線距離の差)が、転入者数の大小により変化する
最終的には以下のような曲線を描きます。
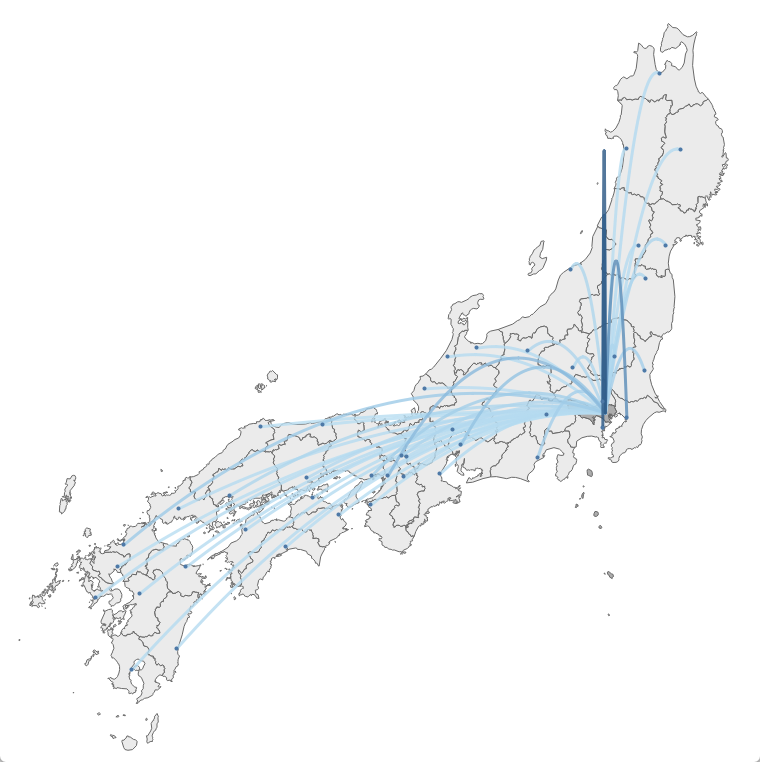
2次ベジェ曲線を使用して曲線を描く
使用する曲線の種類は何でも良いのですが、今回は2次ベジェ曲線を使用します。
Wikipedia: ベジェ曲線
2次ベジェ曲線は3点の座標(P0, P1, P2)を与えれば求まります。 今回の問題設定では
P0: 東京都の座標(経度, 緯度)
P2: 転入元の都道府県の座標(経度, 緯度)
は与えられているので、3点目P1を考える必要があります。
ここでは簡単のために、P1のX座標は、P0とP2の平均値とし、P1のY座標は東京都と転入元都道府県の緯度のうち、大きい方の1.05倍とします。 ただし事前にP0の座標のために、東京都の緯度経度を入力したパラメータ[Tokyo Lat]および[Tokyo Long]を用意しています。
P1 X
(MIN([Longitude])+[Tokyo Long])/2P1 Y
MAX([Tokyo Lat], MIN([Latitude])) * 1.05余談:2次ベジェ曲線のP1の座標について
曲線の始点P0と終点P2はデータから与えられているものとして、曲線の形を決める点P1は、実際のところ任意の値で問題ありません。
P1の値で2次ベジェ曲線がどのように変わるかを視覚的に理解するために、以下のシートを作成しました。 ぜひパラメータ値を変えながら遊んでみてください。 https://tabsoft.co/3uNBuut

ところで、これからTableauで描く曲線は線マークを使用します。 曲線を描くためのデータ点を作成するために、以下のようにデータを結合します。

そして結合したDummyシートにある[t]列を使用して2次ベジェ曲線を描くため、XY座標それぞれのための計算フィールドを作成します。
Bezier X
(1 - MIN([t]))^2*MIN([Longitude])
+ 2*(1 - MIN([t]))*MIN([t])*[P1 X]
+ MIN([t])^2 * [Tokyo Long]Bezier Y
(1 - MIN([t]))^2*MIN([Latitude])
+ 2*(1 - MIN([t]))*MIN([t])*[P1 Y]
+ MIN([t])^2 * [Tokyo Lat]詳細マークに[都道府県]を、線マークにDummyシートからの[t]列を入れ、行と列にそれぞれ作成した計算フィールドを置きます。 簡単のため、ここでは愛知県でフィルターします。

これで2地点を2次ベジェ曲線で結ぶことはできました。
もう少し分かりやすくするために、マップレイヤー等を追加しました。 赤線が作成した2次ベジェ曲線、黒線がMAKELINE関数で描画された線です。

ここまでの内容で一度比較をしてみましょう。
左がMAKELINE関数による可視化、右がベジェ曲線による可視化です。
転入者数が多い神奈川県、埼玉県、千葉県が目立つようになりました。 また各都道府県の線や都道府県庁所在地が選択しやすくなりました。
ただし現在の曲線の高さは全て一律1.05倍のため、色で表現されてはいるものの、各都道府県からの転入者数の大小が少しわかりにくいものになっています。
言い換えれば、転入者数が多かった都道府県だけ曲線がより長くなり視認しやすくなるように変更したいです。
曲線の高さは[P1 Y]で制御されるため、転入者数の大小が反映されるように、この計算フィールドを改修します。
またベジェ曲線も改修後のものを使用するようにします。
Measure
// 転入者数で重み付けをする
SUM([転入者数])Measure Normalized
//[0, 0.2]の範囲で正規化する
([Measure] - WINDOW_MIN([Measure]))
/ (WINDOW_MAX([Measure]) - WINDOW_MIN([Measure]))
* 0.2P1 Y (Adjusted)
MAX([Tokyo Lat], MIN([Latitude]))
* (1 + ZN([Measure Normalized]))Bezier Y (Adjusted)
(1 - MIN([t]))^2*MIN([Latitude])
+ 2*(1 - MIN([t]))*MIN([t])*[P1 Y (Adjusted)]
+ MIN([t])^2 * [Tokyo Lat]ここでは転入者数を0.0 ~ 0.2の範囲となるようMeasure Normalizedで正規化し、その値に1を足したもの(1 + ZN([Measure Normalized]))を、元々の1.05倍の代わりに使用します。
結果を比較してみましょう。左が改修前、右が改修後です。
転入者数が少ない都道府県の曲線の広がりが控えめになり、一方で多い都道府県は線がより広がるようになりました。
神奈川、埼玉、千葉、静岡、愛知県が顕著ですね。
このようにして、距離が近い2地点について、集計値を考慮した曲線を描くことができました。
指標の正負を反映した曲線を描く
次に、曲線を正負が分かれる指標を使用して描画する場合について書きます。
ここでは転入超過数 (転入数 - 転出数)を例にして解説します。
最終的には以下のような可視化を作成します。転入超過数が正の場合 (東京都に入ってきた人の方が多い) 場合には曲線が上向きに、負の場合 (東京都から出ていく人の方が多い) 場合には曲線が下向きになっています。

基本的な作り方は上記までと同じですが、Measure Normalizedに少し修正が必要になります。
Measure
SUM([転入超過数])Measure Normalized
// まずMeasureの絶対値を[0, 0.2]に正規化する
// その後、Measureの符号をかける
(ABS([Measure]) - WINDOW_MIN(ABS([Measure])))
/ (WINDOW_MAX(ABS([Measure])) - WINDOW_MIN(ABS([Measure])))
* 0.2
* SIGN([Measure])転入超過数のような正負どちらも取り得る場合、[0,1]に正規化した場合、負の値も0以上にスケーリングされます。
ただし作成したい曲線は、転入超過数がマイナスの場合は下を向く、つまりP1のY座標がP0とP2よりも0に近くなる必要があり、転入超過数の正負を考慮する必要があります。
これを実現するために、まずは転入超過数の絶対値を[0,1]に正規化し、符号関係ない値の大小自体を[0,1]範囲で比較できるようにします。
その後、[0,1]に正規化された値について「元々プラスマイナスどっちだっけ」を考慮するためにSIGN()をかけます。 最後に0.2をかけ、どの程度曲線を上下に広げるかを調整します。この数字は任意です。
これだけの修正で、曲線が指標の正負を反映するようになりました。
正負それぞれの曲線2本を描画する
最後に、転入数と転出数それぞれを別の線として描画する方法について記載します。
ここでは転入数を上向きの曲線、転出数を下向きの曲線として描画します。
以下は東京都 - 愛知県間についての可視化です。上側の曲線が下側の曲線よりも広がっていることから、転入超過であることが視覚的に分かります。
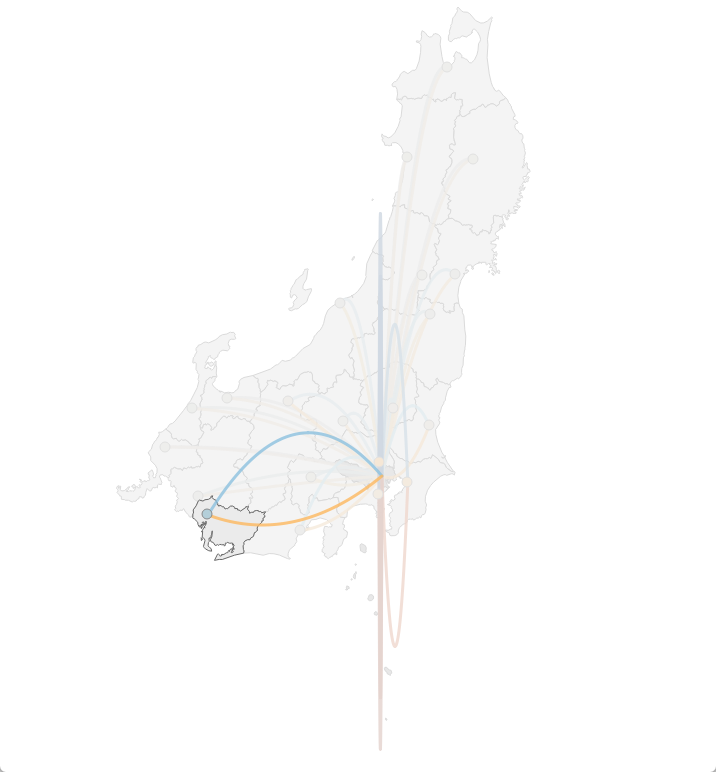
この可視化を作成するためには、各都道府県の組み合わせにおいて、転入数と転出数それぞれの曲線のためのマークが必要になります。
必要なマーク数を用意する方法はいくつかありますが、ここでは簡単のために、転入数と転出数でPivotしたデータをTableau上で用意し、そのデータにDummyシートを同様に結合します。
まず計算フィールドから説明します。
転入数は正の値、転出数は負の値として扱いたいため、以下のようにMeasureを修正します。
Measure
SUM(
IF [Pivot Field Names] = '転入者数'
THEN 1
ELSE -1
END
* [Pivot Field Values]
)正規化も上述の内容と同様に、正負の値を考慮して行います。
Measure Normalized
// (先ほどと同一)
(ABS([Measure]) - WINDOW_MIN(ABS([Measure])))
/
(WINDOW_MAX(ABS([Measure])) - WINDOW_MIN(ABS([Measure])))
* 0.2
* SIGN([Measure])ベジェ曲線のマークについて、詳細マークに[Pivot Field Names]を入れ、曲線が転入者数と転出者数それぞれに描画されるようにします。
また、[Bezier Y]の表計算設定は下図のように、全都道府県とピボットフィールド名を使用するようにします。

[Bezier Y]で設定する表計算設定はそのまま[Measure Normalized]の表計算設定ですが、ここでは全都道府県の転入者数と転出者数を全て考慮して正規化を行うため、上記の設定としてあります。 もし転入者数と転出者数それぞれで正規化を行いたい場合は[Pivot Field Names]のチェックを外してください。
最後に
2019年にMAKELINE関数が出たときからアイデアとしてはあったのですが、やっとBlogに書いてまとめることが出来ました。 直線でも可視化はできますが、MAKELINE関数で世界地図についての分析をしたときの曲線を見ると、日本地図でも曲線を描きたかったんですよね...
ところで今回の記事では、ボリュームの観点からMap Layerなどの扱いについては特に言及をしませんでした。
空間関数やMap Layerなど、Tableauは地図機能が年々拡張されているので、ぜひこの辺りもキャッチアップいただくと良いと思います。
前回の100%を超えるドーナッツチャートの記事もMap Layerが大活躍でした。
ちなみに今回のベジェ曲線については、TableauでJump Plotを作る方法についての記事でも取り上げています。こちらもご興味あればどうぞ。
質問などありましたら、XかLinkedinまでお願いします。

















